Capítulo 2 Trayectorias de sintomatologia depresiva. Modelo Latent Class Mixed Model (LCMM)
2.1 Identificar trayectorias:
Modelos de trayectorias lineales:
Se usa el modelo de 1 clase para fijar los valores iniciales a iterar:
load(file.path('..', 'inputs', 'modelos_lcmm.RData'))Comparación resultados
# Comparar resultados:
resultados_comparados <- summarytable(lcmm3_lin, lcmm4_lin, lcmm5_lin)postprob(lcmm3_lin)##
## Posterior classification:
## class1 class2 class3
## N 461.0 1370.00 82.00
## % 24.1 71.62 4.29
##
## Posterior classification table:
## --> mean of posterior probabilities in each class
## prob1 prob2 prob3
## class1 0.8217 0.1326 0.0458
## class2 0.0617 0.9383 0.0000
## class3 0.1291 0.0000 0.8709
##
## Posterior probabilities above a threshold (%):
## class1 class2 class3
## prob>0.7 77.44 92.85 82.93
## prob>0.8 62.69 88.18 74.39
## prob>0.9 41.43 81.09 59.76
## postprob(lcmm4_lin)##
## Posterior classification:
## class1 class2 class3 class4
## N 392.00 1346.00 98.00 77.00
## % 20.49 70.36 5.12 4.03
##
## Posterior classification table:
## --> mean of posterior probabilities in each class
## prob1 prob2 prob3 prob4
## class1 0.7853 0.1343 0.0521 0.0282
## class2 0.0613 0.9342 0.0045 0.0000
## class3 0.1376 0.0435 0.7797 0.0392
## class4 0.0978 0.0000 0.0248 0.8774
##
## Posterior probabilities above a threshold (%):
## class1 class2 class3 class4
## prob>0.7 69.13 92.35 68.37 83.12
## prob>0.8 51.28 88.19 50.00 75.32
## prob>0.9 27.81 80.76 37.76 61.04
## postprob(lcmm5_lin)##
## Posterior classification:
## class1 class2 class3 class4 class5
## N 129.00 80.00 48.00 1243.00 413.00
## % 6.74 4.18 2.51 64.98 21.59
##
## Posterior classification table:
## --> mean of posterior probabilities in each class
## prob1 prob2 prob3 prob4 prob5
## class1 0.7675 0.0243 0.0432 0.0051 0.1600
## class2 0.0374 0.8124 0.0238 0.0025 0.1239
## class3 0.0970 0.0549 0.8455 0.0000 0.0025
## class4 0.0018 0.0004 0.0000 0.8932 0.1045
## class5 0.0850 0.0456 0.0003 0.1747 0.6945
##
## Posterior probabilities above a threshold (%):
## class1 class2 class3 class4 class5
## prob>0.7 68.22 72.50 75.00 88.17 52.06
## prob>0.8 44.96 58.75 70.83 78.76 22.76
## prob>0.9 27.91 45.00 52.08 64.60 0.00
## kableExtra::kbl(resultados_comparados[,1:4],
digits = 1)| G | loglik | npm | BIC | |
|---|---|---|---|---|
| lcmm3_lin | 3 | -22642.0 | 9 | 45352.1 |
| lcmm4_lin | 4 | -22555.4 | 12 | 45201.5 |
| lcmm5_lin | 5 | -22530.1 | 15 | 45173.5 |
kableExtra::kbl(resultados_comparados[,5:9],
digits = 1)| %class1 | %class2 | %class3 | %class4 | %class5 | |
|---|---|---|---|---|---|
| lcmm3_lin | 24.1 | 71.6 | 4.3 | NA | NA |
| lcmm4_lin | 20.5 | 70.4 | 5.1 | 4 | NA |
| lcmm5_lin | 6.7 | 4.2 | 2.5 | 65 | 21.6 |
2.2 Principales trayectorias
Según criterios de información debería estar entre 4 y 5 clases:
summary(lcmm4_lin)## Heterogenous linear mixed model
## fitted by maximum likelihood method
##
## hlme(fixed = phq9 ~ ola, mixture = ~ola, subject = "idencuesta",
## ng = 4, data = elsoc_salud_long)
##
## Statistical Model:
## Dataset: elsoc_salud_long
## Number of subjects: 1913
## Number of observations: 7518
## Number of latent classes: 4
## Number of parameters: 12
##
## Iteration process:
## Convergence criteria satisfied
## Number of iterations: 40
## Convergence criteria: parameters= 1.4e-06
## : likelihood= 1.5e-06
## : second derivatives= 1e-11
##
## Goodness-of-fit statistics:
## maximum log-likelihood: -22555.4
## AIC: 45134.8
## BIC: 45201.47
##
##
## Maximum Likelihood Estimates:
##
## Fixed effects in the class-membership model:
## (the class of reference is the last class)
##
## coef Se Wald p-value
## intercept class1 1.60697 0.17336 9.269 0.00000
## intercept class2 2.76869 0.17449 15.867 0.00000
## intercept class3 0.23970 0.26032 0.921 0.35717
##
## Fixed effects in the longitudinal model:
##
## coef Se Wald p-value
## intercept class1 11.03683 0.59999 18.395 0.00000
## intercept class2 3.05637 0.17041 17.935 0.00000
## intercept class3 2.61047 0.81512 3.203 0.00136
## intercept class4 19.70159 0.78596 25.067 0.00000
## ola class1 -0.56535 0.18629 -3.035 0.00241
## ola class2 0.46852 0.05640 8.307 0.00000
## ola class3 3.79455 0.32909 11.530 0.00000
## ola class4 -1.22304 0.28494 -4.292 0.00002
##
## coef Se
## Residual standard error: 4.15204 0.03821pred_lcmm4_lin <- predictY(lcmm4_lin, data.frame(ola = 1:4))
plot(pred_lcmm4_lin, ylim = c(0, 27))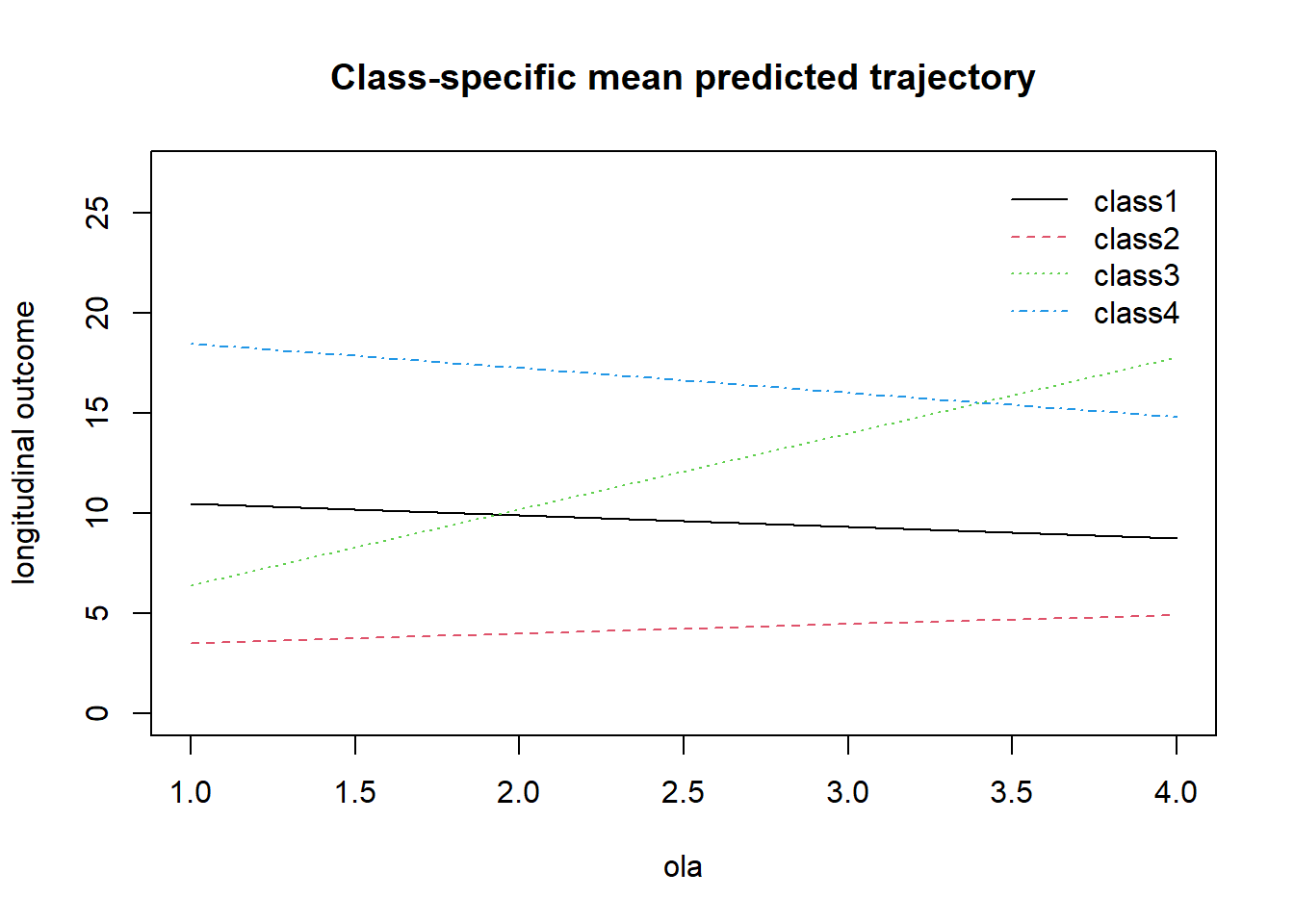
summary(lcmm5_lin)## Heterogenous linear mixed model
## fitted by maximum likelihood method
##
## hlme(fixed = phq9 ~ ola, mixture = ~ola, subject = "idencuesta",
## ng = 5, data = elsoc_salud_long)
##
## Statistical Model:
## Dataset: elsoc_salud_long
## Number of subjects: 1913
## Number of observations: 7518
## Number of latent classes: 5
## Number of parameters: 15
##
## Iteration process:
## Convergence criteria satisfied
## Number of iterations: 44
## Convergence criteria: parameters= 2.8e-05
## : likelihood= 3.6e-05
## : second derivatives= 7e-11
##
## Goodness-of-fit statistics:
## maximum log-likelihood: -22530.07
## AIC: 45090.14
## BIC: 45173.49
##
##
## Maximum Likelihood Estimates:
##
## Fixed effects in the class-membership model:
## (the class of reference is the last class)
##
## coef Se Wald p-value
## intercept class1 -1.13363 0.27773 -4.082 0.00004
## intercept class2 -1.60297 0.20873 -7.680 0.00000
## intercept class3 -2.22890 0.27204 -8.193 0.00000
## intercept class4 0.97249 0.14158 6.869 0.00000
##
## Fixed effects in the longitudinal model:
##
## coef Se Wald p-value
## intercept class1 17.29624 1.14421 15.116 0.00000
## intercept class2 3.60754 0.92278 3.909 0.00009
## intercept class3 19.54451 1.02567 19.055 0.00000
## intercept class4 2.99012 0.19379 15.429 0.00000
## intercept class5 7.05194 0.92131 7.654 0.00000
## ola class1 -2.12546 0.30092 -7.063 0.00000
## ola class2 3.71429 0.33522 11.080 0.00000
## ola class3 -0.59843 0.39151 -1.529 0.12639
## ola class4 0.39012 0.06903 5.652 0.00000
## ola class5 0.49307 0.29497 1.672 0.09460
##
## coef Se
## Residual standard error: 4.08242 0.03853pred_lcmm5_lin <- predictY(lcmm5_lin, data.frame(ola = 1:4))
plot(pred_lcmm5_lin, ylim = c(0, 27))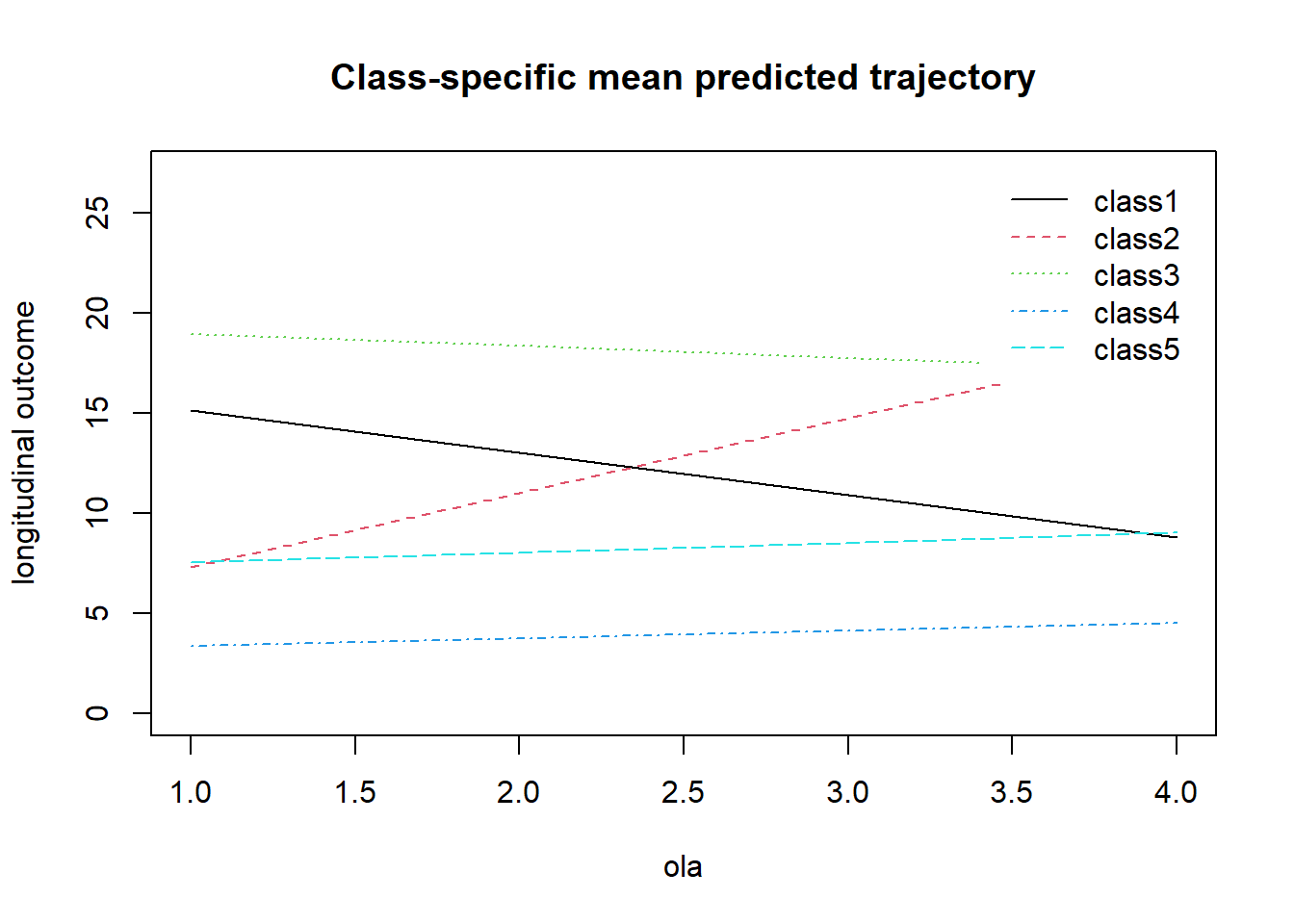
# Librerías básicas
library(tidyverse)
load(file.path('..', 'inputs', 'datos_elsoc_preparados.RData'))
elsoc_salud_modelo <- elsoc_salud_wide